선택 정렬 (SelectSort)
: 가장 작은 것을 선택해서 계속해서 제일 앞으로 보내는 알고리즘
- 가장 원시적이고 기초적인 방법 중 하나
- 데이터의 갯수가 N개일 때 총 몇번의 비교 연산을 해야 되는지 알아야 한다.
- 선택 정렬은 대략 N * (N+1)/2 번 가량의 연산을 수행해야 한다.
- 이를 컴퓨터에서는 가장 큰 차수인 N^2만 보고 O(N^2)이라고 표현한다. 즉, 선택 정렬의 시간 복잡도는 O(N^2)이다
정렬 방법

- 위에 보는 그림과 같이 step 에서는 순서대로 비교하며 index 0의 값을 끝에 값까지 비교한다
- 각각의 step을 거치면서 수행하면서 최솟값을 찾아서 위치를 바꿔준다
- N개의 원소에 대해서는 N-1번을 비교하기 비교한다
def selectionSort(a):
n = len(a)
for i in range(0, n - 1):
min_idx = i
for j in range(i + 1, n):
if a[j] < a[min_idx]:
min_idx = j
a[i], a[min_idx] = a[min_idx], a[i] # swap
d = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
selectionSort(d)
print(d)
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
삽입 정렬 (insertion Sort)
: 자료 배열의 모든 요소를 앞에서부터 차례대료 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입
- 다른 정렬 방식은 무조건 위치를 바꾸는 방식이였다면 삽입 정렬은 필요할 때만 위치를 바꾸게 된다
- 삽입 정렬은 비교적 느린 정렬 알고리즘에 속하며, 복잡한 구조를 가지고 있다
- 만약, 정렬이 되었다고 가장하면 특정한 경우에 따라 빠른 속도를 가지게 되며,
- 삽입 정렬의 시간 복잡도는 O(N^2)이다
정렬 방법


- 다음과 같이 앞에서 부터 차례대로 정렬된 부분과 비교하여, 적절한 위치를 찾아가는 것을 볼 수 있다.
- 특징으로는 계속 비교하므로 리스크 크기가 크면 불리하며, 정렬이 비교적 완성된 데이터의 경우에는 더 유리하다
<python>
array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
for i in range(1, len(array)):
for j in range(i, 0, -1): # 인덱스 i부터 1까지 1씩 감소하며 반복하는 문법
if array[j] < array[j - 1]: # 한 칸씩 왼쪽으로 이동
array[j], array[j - 1] = array[j - 1], array[j]
else: # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
break
print(array)
힙정렬 (Heap Sort)
: 힙트리 구조 (Heap Tree Structure) 를 이용하는 정렬 방법
힙은 이진트리 (Binart Tree: 데이터를 각 노드(node)에 담은 뒤에 노드를 두개씩 이어 붙이는 구조)
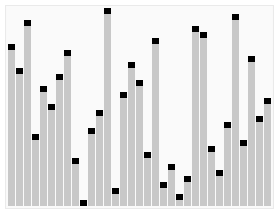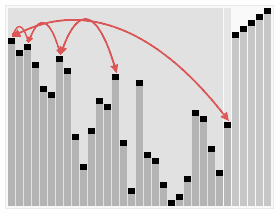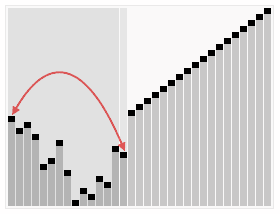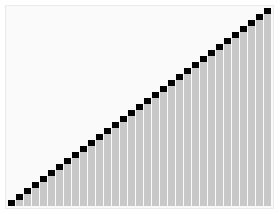
정렬 방법
- n개의 노드에 대한 완전 이진 트리를 구성한다.
- 완전 이진 트리란, 루트 노드부터 부모노드, 왼쪽 자식노드, 오른쪽 자식노드 순으로 구성한다.
- 최대 힙을 구성한다. 최대 힙이란 부모노드가 자식노드보다 큰 트리를 말하는데, 단말 노드를 자식노드로 가진 부모노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.
- 가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.
- 2와 3을 반복한다.

def maxHeap(p):
tmp = arr[p]
while p <= size//2:
c = p * 2
if c < size and arr[c] < arr[c +1]:
c +=1
if tmp > arr[c]: break
arr[p] = arr[c]
p = c
arr[p] = tmp
def Hsort():
global size
for i in range(size//2, 0, -1):
maxHeap(i)
while size > 1:
arr[size], arr[1] = arr[1], arr[size]
size -=1
maxHeap(1)
if __name__ == '__main__':
arr=[0, 35, 19, 55, 60, 34, 10, 30, 22, 15, 32]
size = len(arr)-1
print("Before Sort : ", end='')
print(arr)
Hsort()
print("after Sort : ", end='')
print(arr)
# Before Sort : [0, 35, 19, 55, 60, 34, 10, 30, 22, 15, 32]
# after Sort : [0, 10, 15, 19, 22, 30, 32, 34, 35, 55, 60]
병합 정렬(Merge Sort)
: 주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합친다
- 병합 정렬은 분할 정복 기법과 재귀 알고리즘을 이용한 정렬 알고리즘
- 시간 복잡도는 O(NlogN)이다
- 공간 복잡도는 O(N)
- 다른 정렬 알고리즘과 달리 인접한 값들 간에 상호 자리 교대(swap)이 일어나지 않는다
정렬 방법
리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
- 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 정복(conquer) : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
- 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.
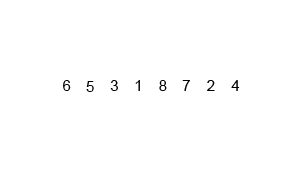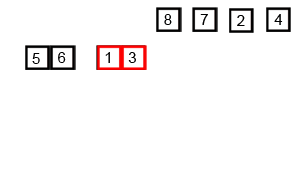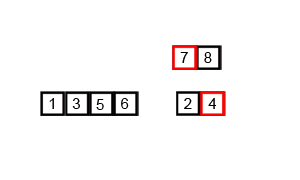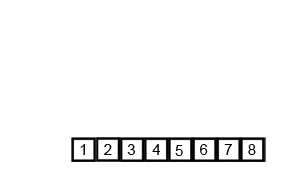
def merge_sort(arr):
if len(arr) <= 1:
return arr
# 배열을 반으로 나누기
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 왼쪽과 오른쪽 배열을 재귀적으로 정렬
left_sorted = merge_sort(left)
right_sorted = merge_sort(right)
# 두 배열을 병합
result = []
i = j = 0
while i < len(left_sorted) and j < len(right_sorted):
if left_sorted[i] < right_sorted[j]:
result.append(left_sorted[i])
i += 1
else:
result.append(right_sorted[j])
j += 1
# 남은 요소들을 추가
result += left_sorted[i:]
result += right_sorted[j:]
return result
퀵 정렬 (Quick Sort)
: 특정한 값을 기준(피벗)으로 큰 숫자와 작은 숫자를 서료 교환한 뒤에 배열을 반으로 나눈다
- 대표적인 분할 정복 알고리즘으로 평균 속도가 O(N*logN)이다
- 하지만 퀵 정렬 최악 시간 복잡도는 O(N^2)이다
정렬 방법
퀵 정렬은 분할 정복(divide and conquer) 방법을 통해 리스트를 정렬한다.
- 리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
- 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다.
이렇게 리스트를 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다. - 분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

- Python
array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while(left <= right):
# 피벗보다 큰 데이터를 찾을 때까지 반복
while(left <= end and array[left] <= array[pivot]):
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while(right > start and array[right] >= array[pivot]):
right -= 1
if(left > right): # 엇갈렸다면 작은 데이터와 피벗을 교체
array[right], array[pivot] = array[pivot], array[right]
else: # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
array[left], array[right] = array[right], array[left]
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)
quick_sort(array, 0, len(array) - 1)
print(array)array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))
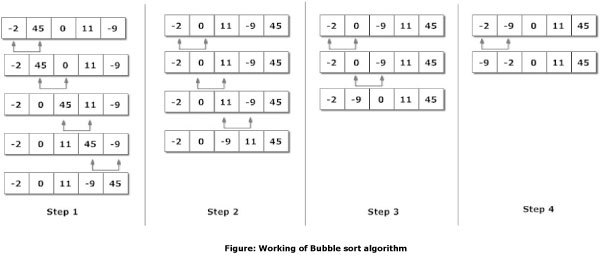
버블 정렬(Bubble Sort)
: 인접한 두 숫자끼리 비교 해서 더 작은 숫자를 앞으로 보내주는 것을 반복
- 인접한 것을 비교해서 가장 큰 값이 맨 뒤로 이동하게 된다
- 제일 큰 값이 뒤로 가게 되면 맨 뒤의 값을 제외하면서 비교를 하면서 제일 큰 값을 뒤로 보낸다
- 정렬 알고리즘 중에서 구현은 가장 쉽지만 가장 비효율적인 알고리즘
- 버블 정렬의 시간 복잡도는 O(N^2) 이다
정렬 방법
def bubble_sort(arr):
n = len(arr)
for i in range(n):
# 리스트를 한 바퀴씩 돌며 인접한 두 원소를 비교하여 정렬
for j in range(n-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
이진탐색 알고리즘
순차 탐색 : 리스트 안에 있는 특정한 데이터를 차기 위해 앞에서부터 테이터를 하나씩 확인하는 방법
이진 탐색 : 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
- 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다
단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 log2N에 비례한다
다시 말해 이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 O(logN)을 보장한다
# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid + 1, end)
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
'programming > python' 카테고리의 다른 글
| [PY] 객체지향 - 상속 (inheritance) (0) | 2022.11.24 |
|---|---|
| [PY] 파이썬의 global과 nonlocal (0) | 2022.11.23 |
| [PY] 파이썬 진수 변환 (0) | 2022.11.22 |
| [PY] 머신러닝과 부동소수점 (0) | 2022.11.21 |
| [PY] 동시성 (멀티스레딩, 멀티프로세싱) (0) | 2022.11.09 |

댓글