회귀와 분류 차이
머신러닝을 통해 해결하려는 문제의 종류에 따라 나눌 수 있는데, 우리가 예측하려는 값의 종류에 따라 회귀와 분류로 구분할 수 있다
값의 종류로는 연속 값(continous value)과 이산 값(discrete value)으로 나눌 수 있다
연속(continuous) 값이란, 말 그대로 연속하는 값을 말한다. 주관신 문제의 답을 쓰듯이, 그값은 0.3이 될 수도 있고 0.31, 0.301, 0.3001 이렇게 끝없이 연속되어 나갈 수 있다. 예를 들면 신장, 체중 등을 의미한다.
이산(Discrete) 값이란, 객관식 문제의 보기처럼 한정된 수로 끊어져 있다. 예를 들면 다음과 같이 "10대/ 20대/ 30대/ 40대/ 50대/ 60대 이상", "e-mail이 스팸인지 아닌지", "어떤 종양이 양성인지 악성인지" 등을 판별하는 것이다.
$$ 회귀는 연속 값을 이용, 분류는 이산 값을 이용$$
즉, 예측할려는 값이 연속 값이면 회귀 문제이며, 예측하려는 값이 이산 값이면 분류 문제 이다
A 보험 회사는 앞으로 고객을 받을 때 어떻게 가격을 책정해야 더 높은 수익을 얻을지 고민 중이다. 이를 해결하기 위해 머신러닝을 활용해보고자 한다. 현재까지 가입한 고객들의 데이터를 학습해서, 새로운 고객의 (적정) 가격을 추론하는 모델을 만들어 보려는 것이다
예시와 같이 추론하려는 값이 '가격' 즉 1,000원 과 같이 유리수로 표현되는 연속 값이다. 따라서 이 머신러닝 모델이 해결하려는 문제는 회귀 문제라고 할 수 있다
B군은 운영 중인 커뮤니티 웹사이트에 올라오는 광고성 게시물을 머신러닝으로 필터링해보려고 한다. 학습된 모델이 추론하려고 하는 것은 새로운 데이터가 들어왔을 때 그것이 광고성인지 아닌 지를 가려내는 것이다. 다음과 같은 예시는 추론하려는 값이 네/ 아니오 중에서 선택하는 이산 값이다. 따라서 이 머신러닝 모델이 해결하는 문제는 분류 문제라고 할 수 있다
위 두 예시와 같이 네 /아니오 두 종류로 구분하는 것이 이진 분류 (binary classification)문제라고 한다. 즉 양성 (positive)와 음성(negative) 로 분류한다는 것이다. 만약 분류하려는 클래스가 두가지 이상이라면, 다항 문제(multi-classification) 문제가 된다. 예를 들어 이미지 데이터에 대해서 사람, 자동차, 도로 중 어느 클래스에 해당하는지 추론하는 것은 다항 분류 문제에 해당한다
다중 분류 학습
현실에서는 많은 다중 분류 학습 문제를 만나게 된다. 어떤 이진 분류 학습법은 직접적으로 다중 분류 방법으로 확장 될 수 있다. 그러나 많은 상황에서 약간의 기초 전략에 기반하여 이진 분류 학습기를 활용해 다중 분류 묹를 해결해야 한다.
일반성을 잃지 않고 N개 클래스 C1, C2, ..., CN이 있다고 가정해 보자. 다중 분류 학습의 기본 아이디어는 분해법이다. 즉, 다중 분류 문제를 몇개의 이진 분류 문제로 분해하여 답을 찾는다.
구체적으로 설명하면 먼저 문제를 분해하고, 분해한 각 이진 분류 문제로 하나의 학습기를 훈련시킨다. 테스트 시에는 분류기들의 예측 결과들을 앙상블하여 최종 다중 분류 결과를 얻는다. 여기서 관건은 어떻게 다중 분류 문제를 붆할 것인가와 어떤 방식으로 다수의 분류기를 앙상블할 것인가이다. 여기서는 주로 분해 전략에 대해 소개한다.
가장 전형적인 분해 전략은 다음 세 가지가 있다.
$$ 일대일, One vs. One. OVO $$
$$ 일대다, One vs. Rest., OvR $$
$$ 다대다, Many vs. Many, MvM $$
다은과 같은 데이터가 있다고 가정하면, D = \({(x_1, y_1), (x_2, y_2), ... , (x_m, y_m)}\), \(y_i \in \left\{ C_1, C_2, ..., C_N \right\} \) 로 정의한다
일대일, One vs. One. OVO
OvO는 N개 클래스를 둘씩 분해한다. 따라서 총 \(N(N - 1)/2\)개의 이진 분류 문제가 새성된다. 예를 들어, OvO가 두 클래스 \(C_i\)와 \(C_j\)로 분류기를 훈련했다면, 해당 분류기는 D 중의 \(C_i\) 클래스 샘픔들을 양성값으로, \(C_j\) 클래스 샘플들을 음성 값으로 분류한다. 테스트 단계에서 새로운 샘플들은 동시에 모든 분류기에서 테스트가 진행되며, 따라서 우리는 총 \(N(N - 1)/2\)개의 분류 결과를 얻게 된다. 최종 결과는 투표를 통해 만들어진다. 즉, 최종적으로 가장 많이 예측된 클래스가 최종 분류 결과값이 된다.

일대다, One vs. Rest., OvR
OvR은 매번 한 분류만 양성값으로 분류하고 남은 모든 클래스들은 음성값으로 분류하여 N개의 분류기를 학습한다. 테스트 단계에서 하나의 분류기가 양성값으로 분류했다면 이에 대응하는 클래스의 레이블을 최종 분류 결과로 정한다. 만약 다수의 분류기가 양성ㄱ밧으로 분류한다면 일반적으로 각 분류기의 예측 실뢰도를 고려하고 신뢰도가 가장 큰 클래스의 레이블을 분류 결과값으로 정ㅎ나다
우리는 OvR은 N개의 분류기만 훈련시키면 되고, OvO는 \(N(N - 1)/2\)개의 분류기를 훈련해야 한다는 점을 쉽게 알 수 있다. 그러므로
OvO의 메모리 사용량과 훈련에 필요한 시간이 OvR에 비해 크다는 점도 알 수 있다. 그러나 훈련단계에서 OvR의 각 분류기가 모든 훈련 데이터를 사용하는 반면, OvO의 각 분류기는 두 클래스의 데이터만 사용한다. 따라서 클래스가 많은 경우 OvO의 훈련 시간은 OvR보다 더 짧다. 예측 성능에 대해서는 구체적인 데이터 분포를 살펴보아야 하지만, 일반적으로 두 학습기의 성능이 비슷하다고 알려져 있다.

다대다, Many vs. Many, MvM
MvM은 매번 몇 개의 클래스를 양성 값에 나머지 기타 클래스는 음성값으로 분해한다. OvO와 OvR은 MvM의 특이 케이스라고 할 수 있다. MvM의 샹성, 음성 클래스 분해 구조는 마음대로 정할 수 없고, 특수한 설계가 바탕으로 되어야 한다.
여기서 가장 자주 사용하는 MvM 방법인 오류 수정 코드(Erro Correcting Output Codes, ECOC)에 대해 알아보자
ECOC는 코딩 사상을 클래스 분해에 적용한 것이다. 그리고 코드 분해 과정에서 최대한 고정 허용 한계 (fault tolerance)를 포함하도록 한다.
클래스 분류는 코딩 매트릭스 (Coding Matrix)를 통해 진핸된다. 다양한 코딩 매트릭스 형식이 있는데, 가장 자주 보이는 형식은 이원코드와 삼원코드이다.
이원코드는 각 클래스를 양성과 음성으로 나누고, 삼원코드는 양성, 음성 외에도 중성이라는 분류를 하나 더 설정한다.
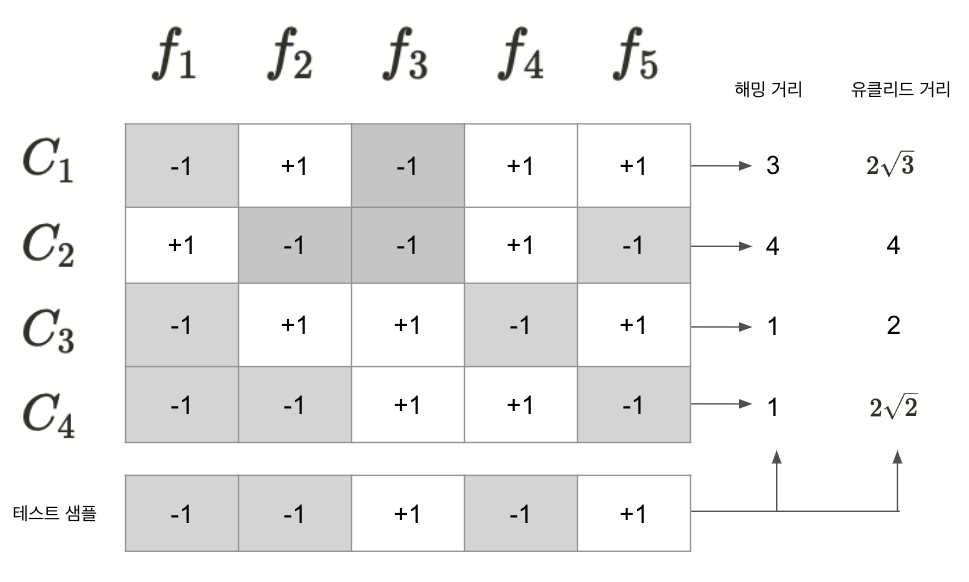
아래의 그림에서 볼수 있듯이 각각의 분류기는 양성 값과 음성 값을 놓는다. 각 분류기의 예측 결과는 하나의 테스트 샘플 코드로 연결된다. 해당 코드들과 비교하여 거리가 가장 짧은 코드에 대응하는 클래스를 예측 결과값이 된다. 결과적으로 예측 결과는 \(C_3\)이 된다.
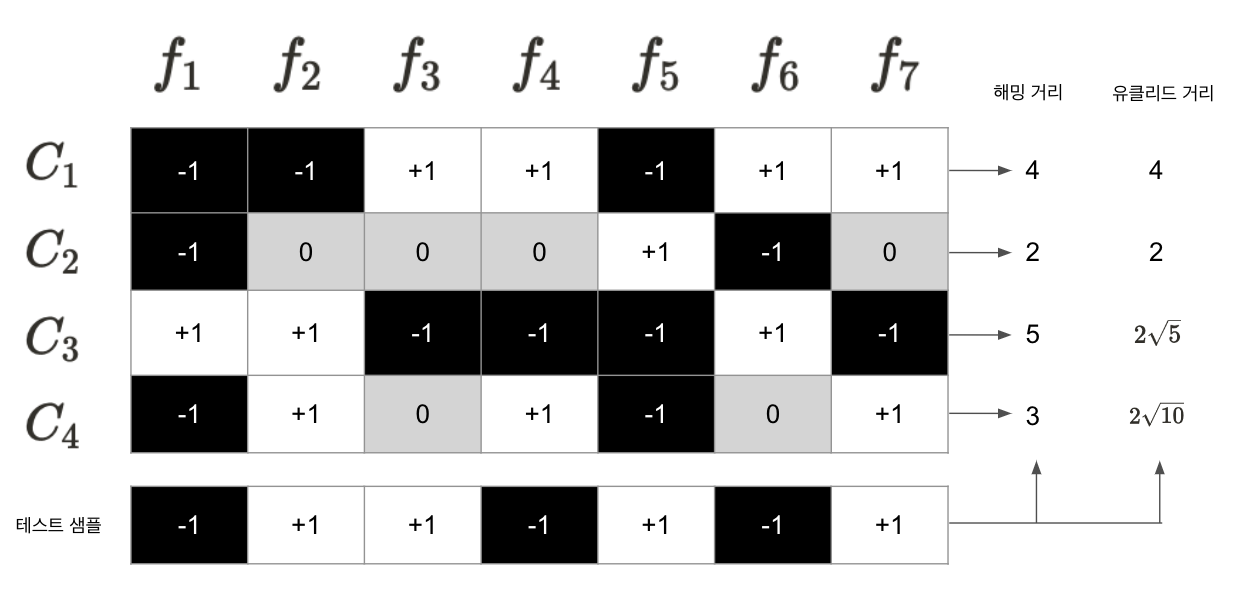
삼원 코드를 보게 된다면 '0'으로 되어 있는 것은 \(f_i\)가 해당 클래스 샘플을 사용하지 않는다는 것을 뜻하며, 아래의 그림과 같이 해당 결과를 얻게 된다.
그렇다면 왜 ECOC라고 부를까? 그 이유는 테스트 단계에서 ECOC 코드는 분류기의 오류에 대한 수정 능력이 있기 때문이다.
참고 자료
1. 단단한 머신러닝
'Machine-Learning > Basic' 카테고리의 다른 글
| [ML] 분류 (Classification) 평가 지표 (0) | 2021.09.05 |
|---|---|
| [ML] 회귀 (Regression) 평가 지표 (0) | 2021.09.05 |
| [ML] Logistic Regression (0) | 2021.03.17 |
| [ML] 회귀(Regression) (0) | 2021.03.15 |
| [ML] 퍼셉트론과 인공신경망 (0) | 2021.03.04 |




댓글