회귀(regression)란 무엇일까?
회귀(regression)는 현대 통계학을 떠받치고 있는 주요 기둥 중 하나이다. 회귀 기반의 분석은 엔지니어링, 의학, 사회과학, 경제학 등의 분야가 발전하는데 크게 기여해왔다. 회귀 분석은 유전적 특성을 연구하던 영국의 통계학자 갈톤 (Galton)이 수행한 연구에서 유래했다는 것이 일반론이다.
갈톤은 부모와 자식 간의 키의 상관 관계를 분석했고, 부모의 키가 모두 클 때 자식의 키가 크긴 하지만 그렇다고 부모를 능가할 정도로 크지 않다고, 부모의 키가 모두 아우 작을 때 그 자식의 키가 작기는 하지만 부모보다는 큰 경향을 발견했다. 부모의 키가 아주 크더라도 자식의 키가 부모보다 더 커서 세대를 이어가면서 무한정 커지는 것이 아니며, 부모의 키가 아주 크더라도 자식의 키가 부모보다 더 작아서 세대를 이어가며 무한정 작아지는 것이 아니라는 것이다. 즉, 사람의 키는 평균 키로 회귀하려는 경향을 가진다는 자연의 법칙이 있다는 것이다. 갈톤은 이러한 현상을 '평균으로의 회귀 (regression toward mean)'라고 했다. 결국, 회귀 분석은 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법이다.
이처럼 회귀 분석을 활용한다면 전체 평균값을 이용하여 누군가의 키를 예측할 수 있으며, 이때 단순히 키의 평균만으로 누군가의 키를 예측하는 것에는 한계가 있기 때문에 키에 영향을 주는 몸무게 등 다른 요인도 활용할 수 있다.
머신러닝에서 회귀분석의 의미
특정한 입력 변수 값을 사용하여 출력 변수의 값을 계산하는 것을 예측 (prediction)문제라고 한다. 예측 문제 중에서 출력 변수의 값이 연속 값인 문제를 회귀(regression) 또는 회귀 분석 (regression analysis) 문제라고 한다.
회귀 분석은 종속 변수 (목표)와 하나 이상의 독립 변수 (예측 변수라고도 함) 간의 미래 사건을 예측하는 방법이다. 예를 들면, 난폭 운전과 운전자에 의해 교통 사고 총 건수 사이의 상관관계를 예측하거나 비즈니스 상황에서는 특정 금액을 광고에 사용했을 때와 그것이 판매에 미치는 영향 사이의 관계를 예측하는 데 사용할 수 있다. 회귀 분석은 머신러닝의 일반적인 모델 중 하나이다. 회귀 분석 모델은 수치적 가치를 추정한다는 측면에서 관측치가 어느 범주에 속하는지를 식별하는 분류 모델과 다르다
ex ) 금융 관련 예측, 판매 및 프로모션 예측, 자동차 테스트, 날씨 분석 및 예측, 시계열 예측
회귀의 종류

회귀의 종류는 독립 변수의 수의 따라서 단순 (Simple), 다중 (Multiple)으로 구분할 수 있으며, 그 아래는 직선의 유무의 따라서 선형(Linear)와 비선형 (Non-Linear)으로 구분할 수 있다.
선형 회귀(Linear Regression)란 무엇일까?
선형 회귀(Linear Regression)는 레전드르(Legendre)가 처음으로 최소제곱법 (least square method)을 1800년대 개발하였고 가우스(Gauss)에 의해서 재발견되면서 200년 넘게 알려져 있는 전통적인 통계 모델로 알려져 있다. 통계학에서 선형 회귀는 종속변수 \(y\)와 한 개 이상의 독립변수(또는 설명 변수) \(x\)와의 선형 상관 관계를 모델링하는 회귀 분석 기법이다. 한 개의 독립 변수에 기반할 경우에는 단순 선형 회귀 (Simple Linear Regression)이라고 하며, 둘 이상의 독립 변수에 기반한 경우에는 다중 선형 회귀 (Multi Linear Regression)라고 한다.
$$ Y = f(X) 일때, \; Y : 종속 변수, X : 독립변수 $$
선형 회귀 는 최대한 정확하게 실제 데이터를 예측하는 선형 모델을 학습하는 것을 목표로 한다.
데이터 세트 D 는 \({(x_1, y_1), (x_2, y_2), ... , (x_m, y_m)}\)으로 정의하고, \(x_i\)는 \((x_{i1}; x_{i2}; ... ; x_{id})\), \(y_i \in \mathbb{R}\) 로 정의한다.
$$ Given \begin{cases} x_i : input & \text{ Find } \ w \text{ and } b \\ y_i : outputs & \end{cases} $$
$$ x = \begin{bmatrix}x_1 \\x_2 \\ \vdots \\x_m \\ \end{bmatrix} , y = \begin{bmatrix}y_1 \\y_2 \\ \vdots \\y_m \\ \end{bmatrix} \approx \hat{y_i} = wx_{i} + b $$
이때 \(\hat{y_i}\)는 예측된 출력값(predicted output)이라 하고, (w, b)는 모델 파라미터(model parameters)라 한다.
입력값에 대해서는 이산 속성(discrete feature) 에 대해서는 속성값에 순서(order)가 있다면 연속값으로 변환해 주어야 한다.
예를 들어, 속성값이 '크다' / '작다' 를 가지는 key라면 {1.0, 0.0} 과 같이 변환해 주고, '높음'/ '중간'/ '낮은' 총 세가지 값을 가지는 변수라면 {1.0, 0.5, 0.0}과 같이 변환해 준다. 만약 '수박'/ '호박'/ '오이' 라는 변숫값이 있다면 (0,0,1), (0,1,0), (1,0,0)과 같이 바꿔준다
선형 회귀는 다음과 같은 함수로 학습한다
$$ f(x_i) = wx_i + b 를 통해 f(x_i) \simeq y_i 을 얻는다 $$
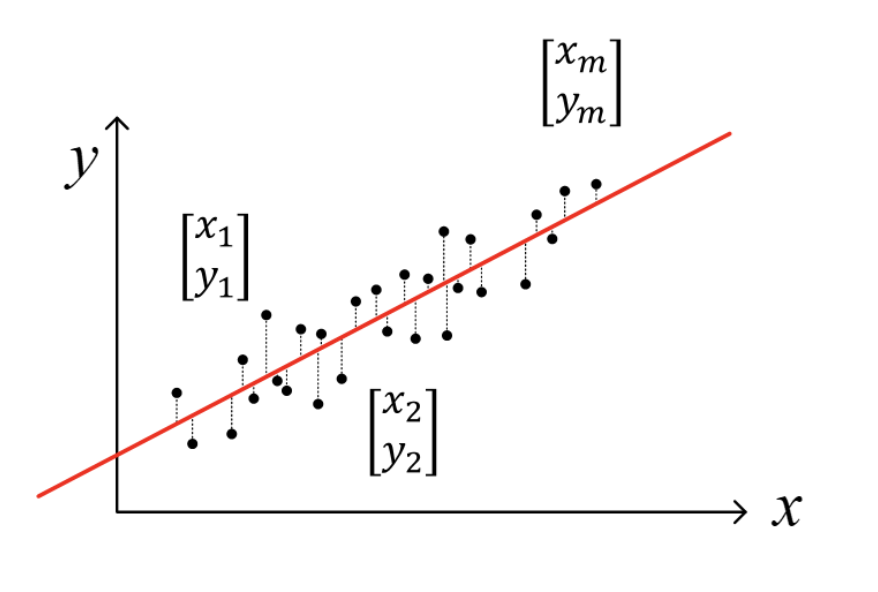
많은 경우에, 선형 모델은 \(y_i\)를 예측하기 위해서 사용되고 있고,
$$ \hat{y_i} = wx_{i} + b $$
$$ \underset{\theta_{0}\theta_{1}}{min}\sum_{i=1}^{m}(\hat{y_i} - y_i)^2$$
위 식과 같은 선형회귀에 대한 식으로 표현할 수 있다.
다중 선형 회귀 (Multiple Linear Regression)
다중 선형 회귀는 하나의 종속 변수\(y \)와 여러 개의 독립 변수 \(x_1, x_2, ..., x_m\) 사이에서의 선형 관계를 모델링한 것인다.
$$ y={\theta_{0}} + {\theta_{1}}{x_1} + {\theta_{2}}{x_2} + ... {\theta_{m}}{x_m} + e $$
이때, \(e\)는 입실론이라고 불리며, 보통은 이것을 noise라고 생각하며, 시스템 상으로 어찌할 수 없는 변동성을 의미한다. 이러한 노이즈는 다중 선형 회귀에서 독립 변수와 종속 변수간의 설명 가능한으로 모델링을 만들어야 하기 때문에 다음과 같이 변화 시킬 수 있다.
$$ y={\hat{\theta_{0}}} + {\hat{\theta_{1}}}{x_1} + \hat{{\theta_{2}}}{x_2} + ... \hat{{\theta_{m}}}{x_m} $$
여기서, \(\hat{\theta_{m}}\)은 회귀 계수 (coefficients) 이라고 불리며, 관계들을 맺어주는 회귀 계수 (coefficients) 를 찾는 것을 목적으로 모델링한다.
이처럼 선형 회귀의 가정은 입력의 독립 변수와 출력(=타켓)의 종속 변수들 간의 항상 선형 관계를 유지해야 하며, 독립 변수와 종속 변수들 간의 1차 항으로 설명 될 수 있으며, 이때 1차 항에 대응하는 최적된 회귀 계수 (coefficients)를 찾는 것을 목적으로 하고 있다.
회귀 계수 (coefficient) 는 어떻게 찾을까?
최소 제곱법 (Least Squares method)
회귀 계수를 찾는 법은 다양하지만, 대표적인 방법으로는 최소 제곱법 (Ordinary Least Square : OLS)있다. 최소 제곱법은 평균 제곱 오차를 최소화하는 방법으로 모델의 해를 구하는 방법이다. 즉, 최소 제곱법의 경우는 실제 타켓(종속) 변수와 모델을 통해 추정된 타켓(종속) 사이에 Square difference를 최소화 하겠다. 선형 회귀에서 최소 제곱법은 샘플과의 유클리드 거리의 합이 가장 작은 하나의 직선을 찾는 것을 목표로 한다.

$$ Actual target : y={\theta_{0}} + {\theta_{1}}{x_1} + {\theta_{2}}{x_2} + ... {\theta_{m}}{x_m} + e $$
$$ Predicted target :y={\hat{\theta_{0}}} + {\hat{\theta_{1}}}{x_1} + \hat{{\theta_{2}}}{x_2} + ... \hat{{\theta_{m}}}{x_m} $$
이처럼, 실제의 타켓 값과 예측할 타켓 값 사이를 최소화를 최소 제곱법으로 진행하게 된다면
$$ min\frac{1}{2}\sum_{i=1}^{n}(y_i -\hat{y_i})^2 $$$$ \frac{1}{2}(y_i - ({\hat{\theta_{0}}} + {\hat{\theta_{1}}}{x_1} + \hat{{\theta_{2}}}{x_2} + ... \hat{{\theta_{m}}}{x_m}))^2$$의 식으로 표현할 수 있다.
위 식을 Matrix Solution을 이용하여 최소제곱법을 풀게 된다면
$$ X : n \times (d + 1) ,\; matrix $$
$$ Y : n \times 1 ,\; vector $$
$$ \hat{\theta} : (d + 1) \times 1, \; vertor $$
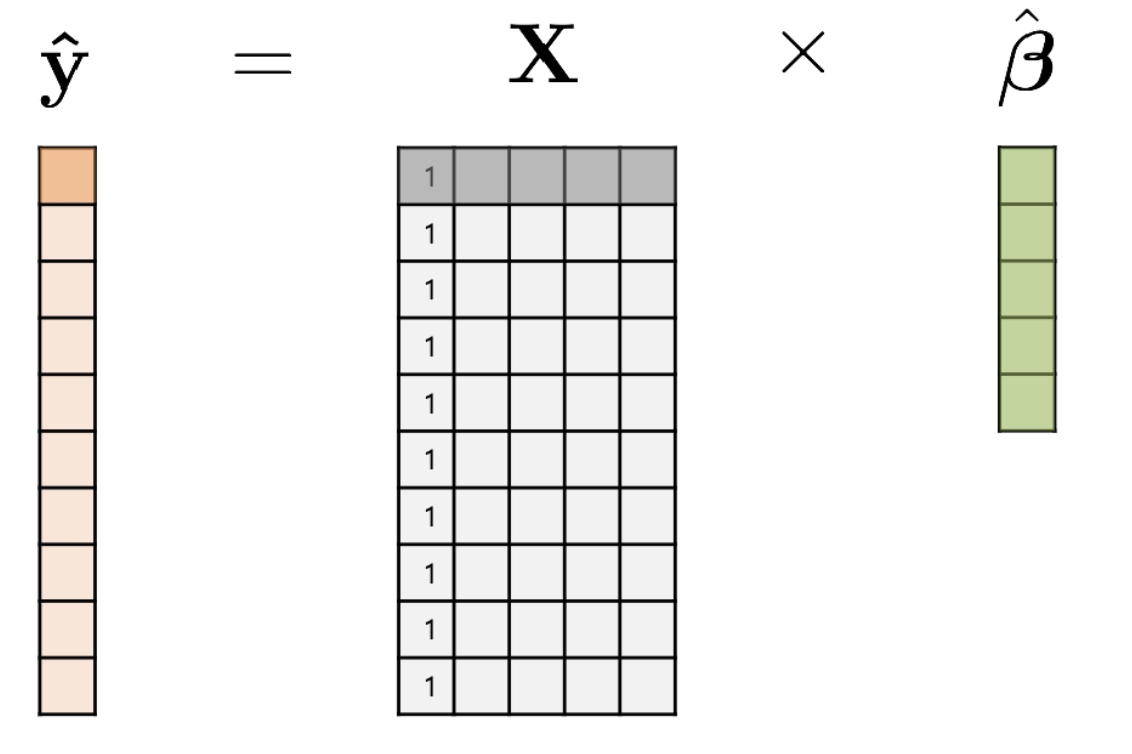
예를 들어, 집에 대한 가격을 예측 한다고 했을 때, n 은실제 집값의 갯수를 의미하며, d 는 집값에 영향을 미치는 요소가 될 수 있다.
위의 요소를 최소제곱법으로 풀이를 하게 된다면
$$ minE(X) = \frac{1}{2}(y-X\hat{\theta})^T(y-X\hat{\theta}) $$
$$ \Rightarrow \frac{\partial E(X)}{\partial \hat{\theta}} = -{X^T}(y-X\hat{\theta}) = 0 $$
$$ X^Ty + X^TX\hat{\theta} = 0 $$
$$ \hat{\theta} = {(X^TX)}^{-1}{X^Ty} $$
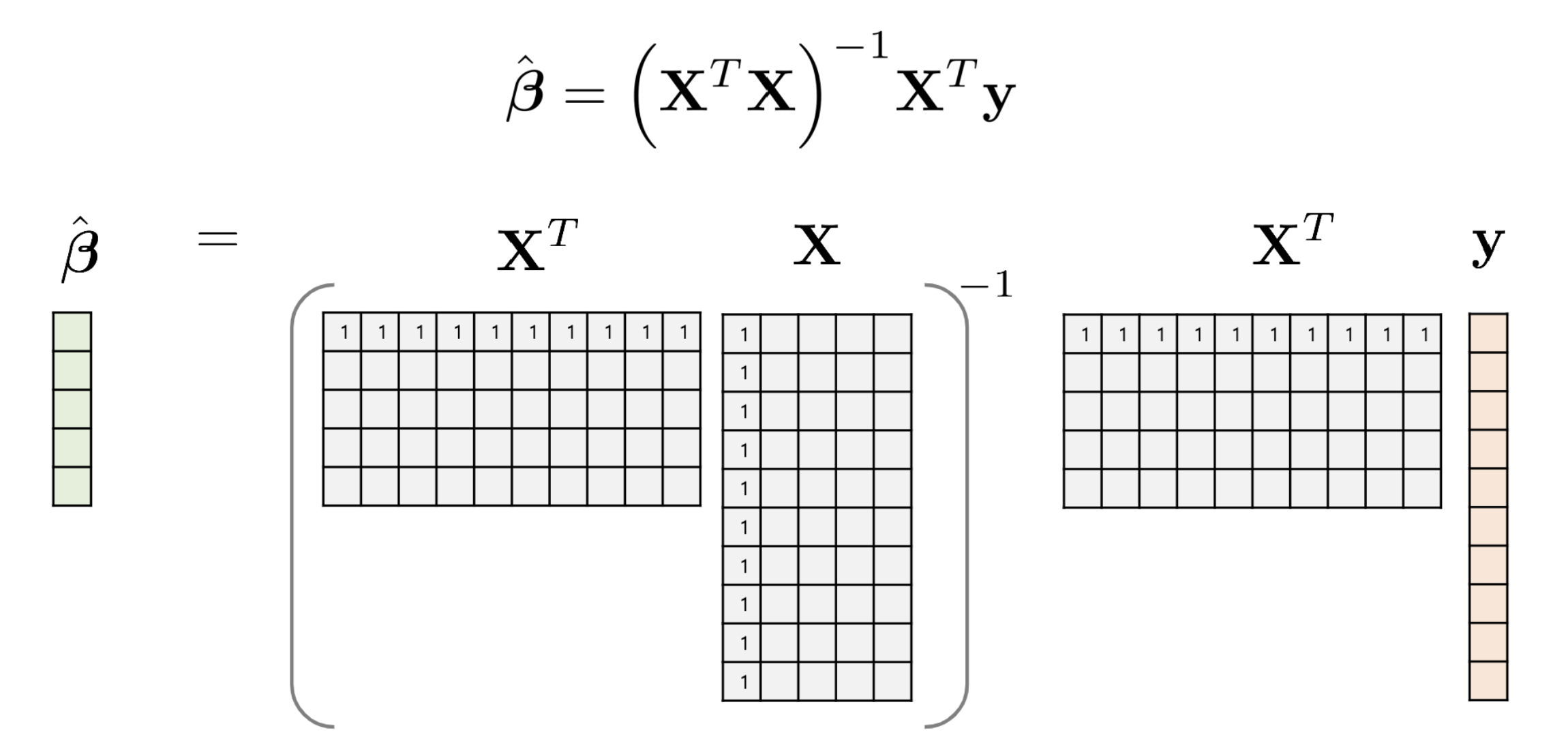
이처럼, 최소 제곱법을 이용하여 적절한 회귀 계수를 찾을 수 있다.
참고자료
1. 고려대 강성범 교수님 : Multiple Linear Regression
2. POSTECH : https://iai.postech.ac.kr/teaching/machine-learning
3. 단단한 머신러닝
4. 패턴 인식과 머신러닝
'Machine-Learning > Basic' 카테고리의 다른 글
| [ML] 회귀 (Regression) 평가 지표 (0) | 2021.09.05 |
|---|---|
| [ML] 분류 (Classification) (0) | 2021.09.05 |
| [ML] Logistic Regression (0) | 2021.03.17 |
| [ML] 퍼셉트론과 인공신경망 (0) | 2021.03.04 |
| [ML] 인공지능(AI) 개요 (0) | 2019.12.05 |




댓글