로버트(Roberts) 마스크
- 로버트 마스크는 대각선 반향으로 1과 -1을 배치하여 구성되며, 나머지 원소의 값이 모두 0이어서 다른 1차 미분 마스크에 비해서 계산이 단순하다. 그리고 한 번만 차분을 게산하기 때문에 차분의 크기가 작고, 이로 인해서 경계가 확실한 에지만 추출하며, 잡음에 매우 민감하다
import numpy as np, cv2
# 회선 수행 함수 - 행렬 처리 방식
def filter(image, mask):
rows, cols = image.shape[:2]
dst = np.zeros((rows, cols), np.float32) # 회선 결과 저장 행렬
xcenter, ycenter = mask.shape[1]//2, mask.shape[0]//2 # 마스크 중심 좌표
for i in range(ycenter, rows - ycenter): # 입력 행렬 반복 순회
for j in range(xcenter, cols - xcenter):
y1, y2 = i - ycenter, i + ycenter + 1 # 관심영역 높이 범위
x1, x2 = j - xcenter, j + xcenter + 1 # 관심영역 너비 범위
roi = image[y1:y2, x1:x2].astype("float32") # 관심영역 형변환
tmp = cv2.multiply(roi, mask) # 회선 적용 - OpenCV 곱셈
dst[i, j] = cv2.sumElems(tmp)[0] # 출력화소 저장
return dst # 자료형 변환하여 반환
def differential(image, data1, data2):
mask1 = np.array(data1, np.float32).reshape(3, 3)
mask2 = np.array(data2, np.float32).reshape(3, 3)
dst1 = filter(image, mask1)
dst2 = filter(image, mask2)
dst = cv2.magnitude(dst1, dst2) # 회선 결과인 두 행렬의 크기 계산
dst1, dst2 = np.abs(dst1), np.abs(dst2) # 회선 결과 행렬 양수 변경
dst = np.clip(dst, 0, 255).astype("uint8")
dst1 = np.clip(dst1, 0, 255).astype("uint8")
dst2 = np.clip(dst2, 0, 255).astype("uint8")
return dst, dst1, dst2
image = cv2.imread("img/edge.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상파일 읽기 오류")
data1 = [-1, 0, 0,
0, 1, 0,
0, 0, 0]
data2 = [ 0, 0, -1,
0, 1, 0,
0, 0, 0]
dst, dst1, dst2 = differential(image, data1, data2) # 회선 수행 및 두 방향의 크기 계산
cv2.imshow("image", image)
cv2.imshow("roberts edge", dst)
cv2.imshow("dst1", dst1)
cv2.imshow("dst2", dst2)
cv2.waitKey(0)

프리윗(prewitt) 에지 검출
- 프리윗 마스크는 원소의 배치가 수직방향으로 구성되어서 수직 마스크라고 하며, 결과 영상에서 에지의 방향도 수직으로 나타낸다
import numpy as np, cv2
def filter(image, mask):
rows, cols = image.shape[:2]
dst = np.zeros((rows, cols), np.float32) # 회선 결과 저장 행렬
xcenter, ycenter = mask.shape[1]//2, mask.shape[0]//2 # 마스크 중심 좌표
for i in range(ycenter, rows - ycenter): # 입력 행렬 반복 순회
for j in range(xcenter, cols - xcenter):
y1, y2 = i - ycenter, i + ycenter + 1 # 관심영역 높이 범위
x1, x2 = j - xcenter, j + xcenter + 1 # 관심영역 너비 범위
roi = image[y1:y2, x1:x2].astype("float32") # 관심영역 형변환
tmp = cv2.multiply(roi, mask) # 회선 적용 - OpenCV 곱셈
dst[i, j] = cv2.sumElems(tmp)[0] # 출력화소 저장
return dst
def differential(image, data1, data2):
mask1 = np.array(data1, np.float32).reshape(3, 3)
mask2 = np.array(data2, np.float32).reshape(3, 3)
dst1 = filter(image, mask1) # 사용자 정의 회선 함수
dst2 = filter(image, mask2)
dst = cv2.magnitude(dst1, dst2) # 회선 결과 두 행렬의 크기 계산
dst = cv2.convertScaleAbs(dst) # 윈도우 표시 위해 OpenCV 함수로 형변환 및 saturation 수행
dst1 = cv2.convertScaleAbs(dst1)
dst2 = cv2.convertScaleAbs(dst2)
return dst, dst1, dst2
image = cv2.imread("img/edge.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상파일 읽기 오류")
data1 = [-1, 0, 1, # 프리윗 수직 마스크
-1, 0, 1,
-1, 0, 1]
data2 = [-1,-1,-1, # 프리윗 수평 마스크
0, 0, 0,
1, 1, 1]
dst, dst1, dst2 = differential(image, data1, data2)
cv2.imshow("image", image)
cv2.imshow("prewitt edge", dst)
cv2.imshow("dst1 - vertical mask", dst1)
cv2.imshow("dst2 - horizontal mask", dst2)
cv2.waitKey(0)

- 결과 image에서 dst1, dst2에서 선명한 에지가 검출된 것을 확인할 수 있으며, 우측 상단의 결과 영상에서 전반적으로 대각선 방향보다 수직과 수평 방향의 에지가 잘 검출하는 것을 확인할 수 있다
소벨(Soble) 마스크
- 소벨 마스크는 에지 추출을 위한 가장 대표적인 1차 미분 연산자 이다. 마스쿠의 구성은 프리위 마스크와 유시하지만 중심 계수의 차분에 대한 비중을 2배로 키운 것이 특징이다.
- 소벨 마스크도 수직 마스크의 회선 결과와 수평 마스크의 회선 결과의 크기로 구성된다. 수직, 수평 방향의 에지도 잘 추출하며, 특히, 중심계수의 차분 비중을 높였기 때문에 대각선 방향의 에지도 잘 검출한다
import numpy as np, cv2
def filter(image, mask):
rows, cols = image.shape[:2]
dst = np.zeros((rows, cols), np.float32) # 회선 결과 저장 행렬
xcenter, ycenter = mask.shape[1]//2, mask.shape[0]//2 # 마스크 중심 좌표
for i in range(ycenter, rows - ycenter): # 입력 행렬 반복 순회
for j in range(xcenter, cols - xcenter):
y1, y2 = i - ycenter, i + ycenter + 1 # 관심영역 높이 범위
x1, x2 = j - xcenter, j + xcenter + 1 # 관심영역 너비 범위
roi = image[y1:y2, x1:x2].astype("float32") # 관심영역 형변환
tmp = cv2.multiply(roi, mask) # 회선 적용 - OpenCV 곱셈
dst[i, j] = cv2.sumElems(tmp)[0] # 출력화소 저장
return dst
def differential(image, data1, data2):
# 입력 인자로 마스크 행렬 초기화
mask1 = np.array(data1, np.float32).reshape(3, 3)
mask2 = np.array(data2, np.float32).reshape(3, 3)
# 사용자 정의 회선 함수
dst1 = filter(image, mask1)
dst2 = filter(image, mask2)
dst = cv2.magnitude(dst1, dst2); # 회선 결과 두 행렬의 크기 계산
# dst1, dst2 = np.abs(dst1), np.abs(dst2) # 회선 결과 행렬 양수 변경
dst = cv2.convertScaleAbs(dst)
dst1 = cv2.convertScaleAbs(dst1)
dst2 = cv2.convertScaleAbs(dst2)
return dst, dst1, dst2
image = cv2.imread("img/edge.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상파일 읽기 오류")
data1 = [-1, 0, 1, # 수직 마스크
-2, 0, 2,
-1, 0, 1]
data2 = [-1,-2,-1, # 수평 마스크
0, 0, 0,
1, 2, 1]
dst, dst1, dst2 = differential(image, data1, data2) # 두 방향 회선 및 크기(에지 강도) 계산
# OpenCV 제공 소벨 에지 계산
dst3 = cv2.Sobel(np.float32(image), cv2.CV_32F, 1, 0, 3) # x방향 미분 - 수직 마스크
dst4 = cv2.Sobel(np.float32(image), cv2.CV_32F, 0, 1, 3) # y방향 미분 - 수평 마스크
dst3 = cv2.convertScaleAbs(dst3) # 절댓값 및 uint8 형변환
dst4 = cv2.convertScaleAbs(dst4)
cv2.imshow("dst- sobel edge", dst)
cv2.imshow("dst1- vertical_mask", dst1)
cv2.imshow("dst2- horizontal_mask", dst2)
cv2.imshow("dst3- vertical_OpenCV", dst3)
cv2.imshow("dst4- horizontal_OpenCV", dst4)
cv2.waitKey(0)

- 수직과 수평 마스크를 적용해서 회선을 수행한 dst1, dst2 영상과 OpenCV에서 제공하는 cv2.Sobel() 함수를 이용해서 수직, 수평 에지를 구한 dst3, dst4의 이미지가 같은 것을 확인할 수 있다
- 영상처리 응용에서 필요한 에지들은 대부분 특정 뱡향의 에지들이다. 따라서 수평이나 수직의 단일 방향 에지를 검출하고자 할때가 종종 있으며, 이 경웨 두 개의 마스크르 같이 적용하지 않고, 하나의 마스크만 적용할 수 있다.
라플라시안 에지 검출
- 2차 미분 연산자로 라플라시안이 있다. 라플라시안은 피에르시몽 라플라스(Pierre-Sinom Laplace) 라는 프랑스의 수학자 이름을 따서 지은 것
- 라플라시안은 함수 f에 대한 그래디언트의 발산으로 정의된다.
- 3x3 크기의 마스크를 예로 라플라시안 마스크 공식에 적용하면, 중심 계수를 4배로 하고 상하 좌우 화소를 중심계수와 반대 부호를 갖게 구성한다. 그리고 마스크 원소의 전체 합은 0이 되어야 한다
- 라플라시안은 중심계수와 4방향 혹은 8방향의 주변화소와 차분을 합하여 에지를 검출하기 대문에 주변 화소에 잡음 성분이 있으면 잡음 성분에 매우 민감하여 실제보다 더 많은 에지를 검출하는 경향이 있다
import numpy as np, cv2
image = cv2.imread("img/laplacian.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상파일 읽기 오류")
data1 = [[0, 1, 0], # 4 방향 필터
[1, 4, 1],
[0, 1, 0]]
data2 = [[-1, -1, -1], # 8 방향 필터
[-1, 8, -1],
[-1, -1, -1]]
mask4 = np.array(data1, np.int16) # 음수가 있으므로 자료형이 int8인 행렬 선언
mask8 = np.array(data2, np.int16)
# OpenCV 함수 cv2.filter2D() 통한 라플라시안 수행
dst1 = cv2.filter2D(image, cv2.CV_16S, mask4)
dst2 = cv2.filter2D(image, cv2.CV_16S, mask8)
dst3 = cv2.Laplacian(image, cv2.CV_16S, 1) # OpenCV 라플라시안 수행 함수
cv2.imshow("image", image)
cv2.imshow("filter2D 4-direction", cv2.convertScaleAbs(dst1))
cv2.imshow("filter2D 8-direction", cv2.convertScaleAbs(dst2))
cv2.imshow("Laplacian_OpenCV", cv2.convertScaleAbs(dst3))
cv2.waitKey(0)

LoG와 DoG
- 라플라시안은 잡음에 민감한 단점이 있다. 그래서 잡음을 먼저 제거하고 라플리사안을 수행한다면 잡음에 강한 에지 검출이 가능한다
- 잡음 제거 방법으로는 미디언 필터링 혹은 최댓값/최솟값 필터링 등을 수행. 그러나 이런 방법들은 비선형 공간 필터링이기 때문에 마스크가 큰 경우 속도 문제가 있다.
- LoG (Laplacian of Gaussian) : 잡음을 제거해 주는 선형 공간 필터를 선택하여 회선을 하고, 그 후에 라플라시안 마스코 회선
- DoG (Difference of Gaussian): 가우시안 수무딩 필터링의 차를 이용하여 에지를 검출
import numpy as np, cv2
image = cv2.imread("img/dog.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상파일 읽기 오류")
gaus = cv2.GaussianBlur(image, (9,9), 0, 0) # 가우시안 마스크 적용
dst1 = cv2.Laplacian(gaus, cv2.CV_16S, 9) # 라플라시안 수행
gaus1 = cv2.GaussianBlur(image, (3, 3), 0) # 가우사안 블러링
gaus2 = cv2.GaussianBlur(image, (9, 9), 0)
dst2 = gaus1 - gaus2 # DoG 수행
cv2.imshow("image", image)
cv2.imshow("dst1 - LoG", dst1.astype("uint8"))
cv2.imshow("dst2 - DoG", dst2)
cv2.waitKey(0)

캐니 에지 검출
- 영상 내에서 잡음은 다른 부분과 경계를 이루는 경우가 많다. 대부분의 에지 검출 방법이 이 잡음들을 에지로 검출하게 된다. 이 문제를 해결하는 방법으로 캐니 에지 검출 기법이 있다
- 캐니 에지 알고리믄은 4단계의 알고리즘으로 구성되어 있다
- 블러링을 통한 노이즈 제거 (가우시안 블러링)
- 화소 기울기 (gradiant)의 강도와 방향 검출(소벨 마스크)
- 비최대치 억제 (non-maximum suppression)
- 이력 임계값(hysteresis threshold)으로 에지 검출
import numpy as np, cv2
def nonmax_suppression(sobel, direct):
rows, cols = sobel.shape[:2]
dst = np.zeros((rows, cols), np.float32)
for i in range(1, rows - 1):
for j in range(1, cols - 1):
# 행렬 처리를 통해 이웃 화소 가져오기
values = sobel[i-1:i+2, j-1:j+2].flatten()
first = [3, 0, 1, 2]
id = first[direct[i, j]]
v1, v2 = values[id], values[8-id]
## if 문으로 이웃 화소 가져오기
# if direct[i, j] == 0: # 기울기 방향 0도
# v1, v2 = sobel[i, j–1], sobel[i, j+1]
# if direct[i, j] == 1: # 기울기 방향 45도
# v1, v2 = sobel[i–1, j–1], sobel[i+1, j+1]
# if direct[i, j] == 2: # 기울기 방향 90도
# v1, v2 = sobel[i–1, j], sobel[i+1, j]
# if direct[i, j] == 3 # 기울기 방향 135도
# v1, v2 = sobel[i+1, j–1], sobel[i–1, j+1]
dst[i, j] = sobel[i, j] if (v1 < sobel[i , j] > v2) else 0
return dst
def trace(max_sobel, i, j, low):
h, w = max_sobel.shape
if (0 <= i < h and 0 <= j < w) == False: return # 추적 화소 범위 확인
if pos_ck[i, j] == 0 and max_sobel[i, j] > low:
pos_ck[i, j] = 255
canny[i, j] = 255
trace(max_sobel, i - 1, j - 1, low)# 추적 함수 재귀 호출 - 8방향 추적
trace(max_sobel, i , j - 1, low)
trace(max_sobel, i + 1, j - 1, low)
trace(max_sobel, i - 1, j , low)
trace(max_sobel, i + 1, j , low)
trace(max_sobel, i - 1, j + 1, low)
trace(max_sobel, i , j + 1, low)
trace(max_sobel, i + 1, j + 1, low)
def hysteresis_th(max_sobel, low, high): # 이력 임계값 수행
rows, cols = max_sobel.shape[:2]
for i in range(1, rows - 1): # 에지 영상 순회
for j in range(1, cols - 1):
if max_sobel[i, j] > high: trace(max_sobel, i, j, low) # 추적 시작
image = cv2.imread("img/canny.jpg", cv2.IMREAD_GRAYSCALE)
if image is None: raise Exception("영상 파일 읽기 오류")
pos_ck = np.zeros(image.shape[:2], np.uint8)
canny = np.zeros(image.shape[:2], np.uint8)
# 사용자 정의 캐니 에지
gaus_img = cv2.GaussianBlur(image, (5, 5), 0.3)
Gx = cv2.Sobel(np.float32(gaus_img), cv2.CV_32F, 1, 0, 3) # x방향 마스크
Gy = cv2.Sobel(np.float32(gaus_img), cv2.CV_32F, 0, 1, 3) # y방향 마스크
sobel = np.fabs(Gx) + np.fabs(Gy) # 두 행렬 절댓값 덧셈
# sobel = cv2.magnitude(Gx, Gy) # 두 행렬 벡터 크기
directs = cv2.phase(Gx, Gy) / (np.pi / 4)
directs = directs.astype(int) % 4
max_sobel = nonmax_suppression(sobel, directs) # 비최대치 억제
hysteresis_th(max_sobel, 100, 150) # 이력 임계값
canny2 = cv2.Canny(image, 100, 150) # OpenCV 캐니 에지
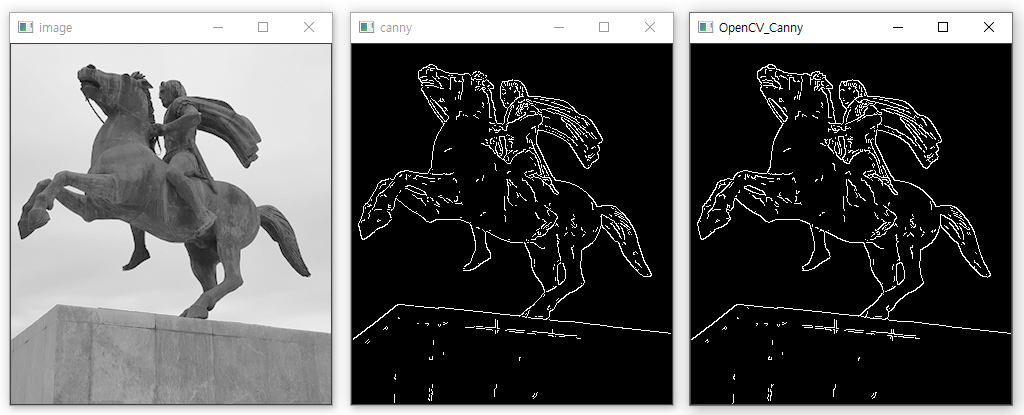
cv2.imshow("image", image)
cv2.imshow("canny", canny) # 사용자 정의 캐니
cv2.imshow("OpenCV_Canny", canny2) # OpenCV 캐니 에지
cv2.waitKey(0)
'Image Processing > OpenCV' 카테고리의 다른 글
| [OpenCV] 모폴로지 (morphology) (0) | 2022.11.25 |
|---|---|
| [OpenCV] 필터링 (Filtering) (0) | 2022.11.25 |
| [OpenCV] 블러링과 샤프닝 (0) | 2022.11.24 |
| [OpenCV] 03. 화소처리 (컬러 공간 변환) (0) | 2022.11.23 |
| [OpenCV] 02. 화소처리 (히스토그램) (0) | 2022.11.23 |




댓글