Transformer의 인코더의 이해

트랜스포머는 N개의 인코더가 쌓인 형태다. 인코더의 결괏값은 그 다음 인코더의 입력값으로 들어간다.
인코더는 N개로 쌓인 형태로 보여준다. 각 인코더의 결괏값은 그 위에 있는 인코더의 입력값으로 들어간다. 가장 마지막 있는 인코더는 결과값이 입력값의 최종 표현 결과가 되는 것이다. 최초 인코더에 대한 입력값으로는 입력 문장을 넣게 되고, 최종 인코더의 결과값으로 입력 문장에 따르는 표현 결과를 얻는 것이다

트랜스포머 관련 논문인 "Attention Is All You Need"를 보면 N=6개로 인코더를 6개 누적해서 쌓아 올린 형태를 표현한 것이다. 하지만 N을 다양한 값으로 지정해 인코더의 형태를 바꿀 수 있다.
그럼 인코더는 어떤 원리로 작동할까? 입력 문장으로 어떤 결과값을 생성하는 가? 이를 이해하려면 먼저 인코더의 구성 요소를 이해해야 한다. 인코더의 구성요소를 포괄적으로 표현하면 다음과 같다

인코더의 구성 요소를 보면 모든 인코더 블록은 형태가 동일하다.
Positional Encoding

Transformer의 네트워크은 Sequence한 CNN와 RNN을 사용하지 않기 때문에 순서 정보를 지정해야 한다. 단어 단위로 문장을 입력하는 대신에 문장 안에 있는 모든 단어를 병렬 (parallel)형태로 입력하며, 병렬로 단어를 입력하는 것은 학습 시간을 줄이고 RNN의 장기 의존성 문제를 해결하는데 도움이 된다.
하지만 트랜스포머에서 단어를 병렬로 입력하면 한 가지 문제가 발생한다. 그것은 바로 단어의 순서 정보가 유지되지 않은 상태에서 문장의 의미를 어떻게 이해할 수 얐느냐는 점이다.
문장의 의미를 이해하기 위해서는 단어의 순서 (문장의 단어의 위치 정보)가 매우 중요하다.
만약 'I am good'이라는 문장으로 처음에 문장 안의 각 단어에 대해 임베딩 값을 얻는다. 이때 임베딩의 차원을 \(d_model\)이라고 한다. 여기서 임베딩 차원의 값을 4라고 하면 문장에 대한 입력 행의 차원은 [문장 길이 x 임베딩 차원] = [3 x 4]가 된다.
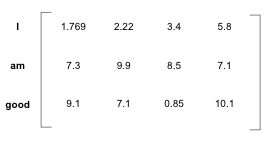
입력 행렬 (임베딩 행렬) 만으로는 순서의 정보를 이해할 수 없기 때문에, 문장의 의미를 의해할 수 있도록 단어의 순서 (단어의 위치)를 표현하는 정보를 추가로 제공해야 한다. 이를 위해 인코딩이라는 새로운 방법을 활용한다.
Positional Encoding이라는 이름에서 알 수 있듯이 문장에서 단어의 위치( 단어의 순서)를 나타내는 인코딩이다.

위치 인코딩 행렬 P의 차원은 입력 행렬 X의 차원과 동일하다. 즉 입력 행렬에 위치 인코딩을 더한 후 네트워크에 입력하는 것이다.

이제 입력 행렬은 단어의 임베딩 뿐 아니라 문장의 단어 위치 정보도 포함하게 되는 것이다.
그럼 Positional Encoding의 P는 어떻게 계산되는 것일까? "Attentions Is All You Need"의 논문에서는 위치 인코딩을 계산하는데 사인파 함수 (sinusoidal function)를 사용했다
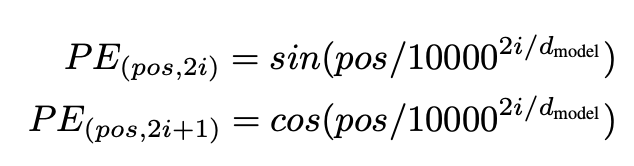
위의 식을 보면 pos는 문장에서 단어위 위치를 의미하고, i는 해당 위치의 임베딩을 의미한다.
$$ \begin{align*}
I \\
am \\
good \\
\end{align*}\begin{bmatrix}
sin(\frac{pos}{10000^0}) & cos(\frac{pos}{10000^0}) & sin(\frac{pos}{10000^{\frac{2}{4}}}) & cos(\frac{pos}{10000^{\frac{2}{4}}})\\
sin(\frac{pos}{10000^0}) & cos(\frac{pos}{10000^0}) & sin(\frac{pos}{10000^{\frac{2}{4}}}) & cos(\frac{pos}{10000^{\frac{2}{4}}}) \\
sin(\frac{pos}{10000^0}) & cos(\frac{pos}{10000^0}) & sin(\frac{pos}{10000^{\frac{2}{4}}}) & cos(\frac{pos}{10000^{\frac{2}{4}}})\\
\end{bmatrix}$$
위의 행렬에서 볼 수 있듯이, 위치 인코딩에서 i의 값이 짝수인 경우 sin 함수를 i의 값이 홀수 인 경우 cos 함수를 사용한다. 이 행렬을 간단하게 표현하면 다음과 같다
$$\begin{align*}
I \\
am \\
good \\
\end{align*}\begin{bmatrix}
sin(pos) & cos(pos) & sin(\frac{pos}{100}) & cos(\frac{pos}{100})\\
sin(pos) & cos(pos) & sin(\frac{pos}{100}) & cos(\frac{pos}{100})\\
sin(pos) & cos(pos) & sin(\frac{pos}{100}) & cos(\frac{pos}{100})\\
\end{bmatrix}$$
입력 문장에서 단어 'I'는 0번째 위치하고, 'am'은 1번째 위치, 'good'은 2번째 위치이다. pos 값을 위치 정보로 대체하면 다음과 같이 표현할 수 있다.
$$ \begin{align*}
I \\
am \\
good \\
\end{align*}\begin{bmatrix}
sin(0) & cos(0) & sin(\frac{0}{100}) & cos(\frac{0}{100})\\
sin(1) & cos(1) & sin(\frac{1}{100}) & cos(\frac{1}{100})\\
sin(2) & cos(2) & sin(\frac{2}{100}) & cos(\frac{2}{100})\\
\end{bmatrix} $$
따라서 위치 인코딩 P는 다음과 같은 행태를 띤다

위치 인코딩 (Positional Encoding)를 계산한 후 임베딩 행렬 X에 대해 요소별 합 (element-wise addition)을 수행한 후 인코더(encoder)의 입력 행렬로 입력한다.
셀프 어텐션의 작동 원리 이해하기
쿼리 (Q), 키 (K), 밸류(V) 행렬 계산 방법과 해당 행렬을 입력 행렬로 얻을 수 있다는 것을 배웠다. 이제 쿼리, 키, 밸류 행렬을 셀프 어텐션에 어떻게 사용하는지 보자.
앞에서 단어의 표현을 계산하기 위해 셀프 어텐션은 각 단어를 기준으로 주어진 문장에 있는 모든 단어와 연결하는 과정을 수행한다는 사실을 배웠다. 'I am good'이라는 문장을 예로 들어보자, 단어 'I'의 표현을 계산하면 아래의 그림처럼 단어 'I' 와 전체 문장에 있는 단어와 연결하는 과정을 수행한다
$$ 그림 $$
위와 같은 방법을 적용하는 이유는 무엇일까?
특정 단어와 문장 내에 있는 모든 단어가 어떤 연관이 있는지를 이해하면 좀 더 좋은 표현을 학습시키는 데 도움이 된다. 이제 셀프 어텐션이 쿼리 (Q), 키 (K), 밸류(V) 값을 사용해 특정 단어와 문장 내에 있는 모든 단어를 연결하는 방법을 알아본다.

$$ z = softmax(\frac{QK^T}{\sqrt{d_k}})V $$
셀프 어텐션의 자세히 설명하기 전에 각 단계에 대해 설명하면
1. 쿼리 행렬과 키 행렬 간의 내적을 계산하고 \(Q\cdot K^T\) 유사도 값을 산출
2. \(Q\cdot K^T\)를 키 행렬의 차원의 제곱근 \(\sqrt{d_k}\)로 나눔
3. 스코어 행렬에 소프트맥스 함수를 적용해 정규화 작업을 진행 \(softmax(\frac{QK^T}{\sqrt{d_k}})\)
4. 마지막으로 스코어 행렬에 밸류 행렬을 콥해 어텐션 행렬 Z를 산출
1단계
쿼리 행렬과 키 행렬 간의 내적을 계산하고 \(Q\cdot K^T\) 유사도 값을 산출

쿼리 행렬 \(Q\)와 키 행렬 \(K^T\) 내적은 다음과 같이 계산할 수 있다
$$ \begin{bmatrix}
q_1\cdot K_1 & q_1\cdot K_2 & q_1\cdot K_3 \\
q_2\cdot K_1 & q_2\cdot K_2 & q_2\cdot K_3 \\
q_3\cdot K_1 & q_3\cdot K_2 & q_3\cdot K_3 \\
\end{bmatrix} $$
그럼 해당 내적을 다음과 같이 구할 수가 있다

이때 쿼리와 키 행렬 사이 내적을 계산하는 이유는 무엇일까? 연산 결과는 정확히 무엇을 의미할까?
\(Q\cdot K^T\)의 첫 번째 행(row)을 보자.
첫 번째 행은 쿼리 벡터 \(q_1 (I)\) 과 키 벡터 \(k_1 (I)\), \(k_2 (am)\), \(k_3 (good)\)의 내적을 계산한다는 것을 알 수 있다.
두 벡터 사이의 내적을 계산하면 두 벡터가 얼마나 유사한지를 알 수 있다.
즉 쿼리 벡터()와 키 벡터() 사이의 내적을 계산하는 것은 쿼리 벡터() 와 키 벡터 () 사이의 유사도를 계산한 것이다.
\(Q\cdot K^T\) 행렬의 첫 번째 행을 보면 단어 I는 단어 am과 good 보다 자신 (I)과 연관성이 더 높은 것을 알 수 있다.
\(q_1\cdot K_1\)의 내적 값이 \(q_1\cdot K_2\), \(q_1\cdot K_3\) 보다 높기 때문이다.
2단계
다음 단계는 \(Q\cdot K^T\) 행렬의 키 벡터 차원으 제곱근 갑승로 나눈 것이다.
이와 같은 방법을 적용하면 안정적인 정삿값(gradient)을 얻을 수 있다
\(d_k\) 를 키 벡터의 차원 (dimension)이라고 하자. 그러면 \(Q\cdot K^T\) 을 \(\sqrt{d_k}\)로 나누면 된다.
해당 키 벡터의 차원 64의 제곱근인 8로 \(Q\cdot K^T\)을 나눈다

3단계
이전 단계에서 계산한 유사도 값은 비정규화된 형태 (unnormalized form)다. 따라서 소프트 맥스 함수(softmax function)를 사용해 정규화 작업을 진행한다. 소프트 맥스 함수를 적용하면 전체 값의 합은 1이 되며 각 0과 1사이의 값을 갖는다.
2단계 결과에 소프트 함수를 적용하면 다음과 같다

이러한 행렬을 스코어 (Socre) 행렬이라고 한다. 위 점수를 바탕으로 문장 내에 있는 각 단어가 문장에 있는 전체 단어와 얼마나 연관되어 있는지 알 수 있다.
예를 들어 스코어 행렬의 첫 행을 보면 단어 I는 자기 자신과 90%, 단어 am 과는 10% 단어 good과는 3% 관련되어 있다는 것을 알 수 있다
4단계
지금까지 쿼리, 키 행렬에 대해 내적을 계산하고, 소프트 맥스 함수를 사용해 내적값에 대한 정규화 작업을 진행했다. 그 다음 과정은 어텐션(Z) 행렬을 계산하는 것이다
어텐션 (attention) 행렬은 문장의 각 단어의 벡터 값을 갖는다. 앞에서 계사한 스코어 행렬인 \(softmax(\frac{QK^T}{\sqrt{d_k}})\) 에 밸류 행렬 (V)을 곱하면 어텐션(Z) 행렬을 구할 수 있다.

어탠션 (Z) 행렬은 각 점수를 기준으로 가중치가 부여된 벡터의 합으로 계산한다.

위 그림처럼 단어 'I'의 셀프 어텐션 \(Z_1\)은 각 벨류 벡터 값의 가중치 합으로 계산된다. 즉, \(Z_1\)의 값은 밸류 벡터 \(v_1 (I)\) 의 90% 값과 밸류 벡터 \(v_2 (am)\)의 70% 값과 밸류 벡터 \(v_3 (good)\)의 3% 값의 합으로 구한다.
이처럼 셀프 어텐션 방법을 적용하면 단어가 문장 내에 있는 다른 단어와 얼마나 연관성이 있는지를 알 수 있다
셀프 어텐션은 쿼리와 키 벡터의 내적을 계산한 다음 \(\sqrt{d_k}\)로 나누기 때문에 스케일 닷 프로덕트 (scaled dot product) 어텐션이라고 부른다.
'Machine-Learning > NLP (Natural Language Processing)' 카테고리의 다른 글
| [NLP] 멀티 헤드 어텐션(multi-head attention) 원리 (2) | 2022.11.06 |
|---|---|
| [NLP] Transforemr - 피드포워드, add와 Norm (0) | 2022.11.06 |
| [NLP] Transformer-Overview (0) | 2022.10.11 |
| [NLP] Seq2Seq (0) | 2022.10.04 |
| [NLP] LSTM /GRU (0) | 2022.09.29 |




댓글